I had students working in groups of 3-4 and in the middle of the table was a plethora of manipulatives...a sampling of pretty much everything I have in my cabinets. I gave each group a note card with a fraction multiplication problem and the following prompt: "Use the stuff at your table to model your multiplication problem as many different ways as you can."
I'll be honest, I had pretty high expectations of what I'd get. We've been doing What's Your Story every week since the start of school and we've had many conversations about what a fraction of a group could look like. Unfortunately, this is what most groups did:
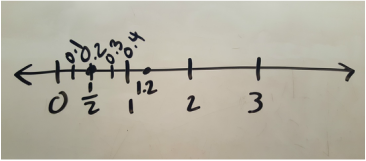
I decided to take a step back and discuss as a class what 1/2 x 1/2 means...1/2 of a group of 1/2. I asked each group to show a way to model it. Things went a little better, but I'll be honest...after the first flop, I was feeling defeated...I just wasn't as excited as I was at the beginning of the lesson. I was having that initial internal struggle with myself:
| Do I spend time solidifying what multiplying fractions means before adding in decimals and negatives? Do I say "screw it" and just remind them, "Hey! Remember that you just multiply across? Yes, the easiest thing you ever have to do with fractions can be completely convoluted and confusing by using these models I'm trying to force on you in order to glean some understanding of what's happening to the numbers???" How soon do I start throwing in mixed numbers? It's almost November and I'm STILL on Unit 1! WTF am I doing??? |
I'd like to say that after that first failure I was able to change things up for the other classes in a way that made things wonderful for them and me...unfortunately, even with the minor changes I made to the lesson (like starting with the 1/2 x 1/2 conversation) the results were pretty much the same. My lower students were getting confused with the model. The higher students were annoyed that I was even asking them to model. It was just, overall, not a great math day.
Ideally, this is the part of the blog where I'd talk about what I'd do differently...how I'd adjust my lesson for next year...but at this point my brain isn't ready to process that. Right now I'm trying to think about what went so wrong...what did I do differently from years past to make this lesson flop so hard. If I ever figure it out, I'll let you know.
Thanks for reading.


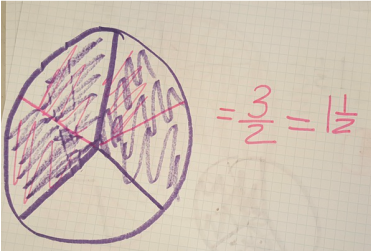

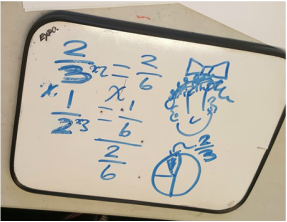

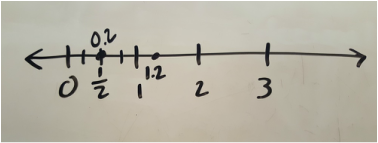
 RSS Feed
RSS Feed
