Or The last Math teacher to ride this train...
I would give students some parallelograms, triangles and trapezoids and tell them what to do:
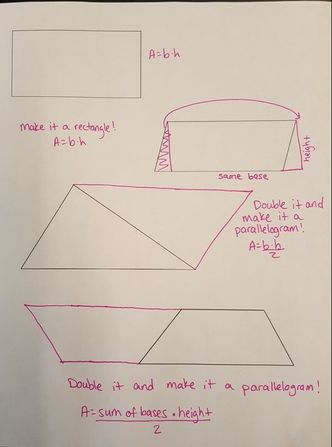
Parallelogram: Cut off this piece and make it into a rectangle! Whoa!
Triangle: Make a copy, flip it over and match the sides to make a parallelogram! Whoa x 2!
Trapezoid: Make a copy, flip it over and match the sides to make a parallelogram! Whoa x 3!
Jump to the trapezoid section to get to the really interesting part!
Parallelograms
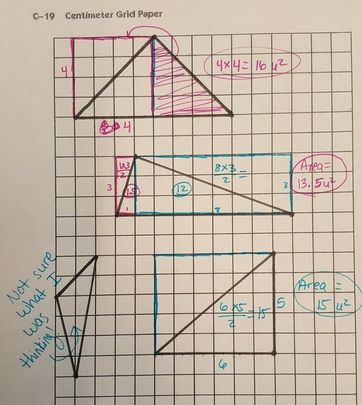
1. Count squares and estimate partial squares. (Not very accurate or easy without grids.)
2. Put rectangles around the triangular parts of the parallelogram and find the areas separately. (Not going to be useful when students are given the measurements.)
3. Cut off the triangular piece on one side and fit it in the empty space of the parallelogram to make a rectangle. (Yay! Someone got it!)
I put a blank parallelogram on the board and asked students what measurements they would like in order to find the area. I gave them all they asked for. Then, I gave them a parallelogram with my choices of measurements and asked them to find the area.
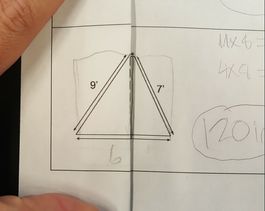
Triangles
1. Count the squares and estimate partial squares (only 1 or 2 students per class stuck to this method.)
2. Cut the triangle in half and fit the piece in the missing spot (only worked for isosceles triangles.)
3. Split the triangle into 2 right triangles and find the areas of each separately. (This was the favorite method.)
4. Double the triangle and make it into a parallelogram, make the parallelogram into a rectangle and then find half that area. (Most students did this with the right triangle, but only some with the other types.)
Ergo, base times height divided by 2. Got the same equation with a different than my usual method.
Trapezoids
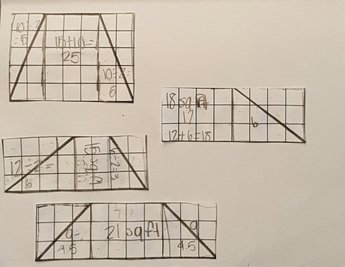
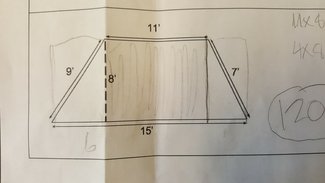
When I gave the trapezoids on grid paper all I heard was "this is so easy!" "I love trapezoids!" And I kept thinking...ha...just wait! Every student solved them the same way by splitting it into 3 parts: Two triangles and a rectangle in the middle.
Short base * height + (long base - short base) * height / 2
I know this formula doesn't match the formula they will be given on any assessment. I don't know that any of the students will even remember the formula they created. I don't know how many students will be able to reproduce what we did a year from now. But I know I let my kids roll with something and they came up with something wonderful.

 RSS Feed
RSS Feed
