Talking about squares...
- Most groups were able to rationalize that a 2x2 was the only possible answer for question 1, but thought if you could make a big enough square you'd be able to make another for question 2.
- One group determined it was impossible to make a square other than 8x8 where the perimeter was half the area because after the 8x8 square the area was increasing faster than the perimeter.
- After a class discussion about questions 1 and 2, I asked again if they could come up with another possible square for each and if not, why. Most groups still thought they could create another square for number 2, so I brought out Desmos.
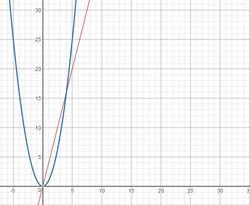
- "WHAT???"
- "It's curved!"
- "Wait, it doesn't go in to the negatives."
- Students picked up on question 3 pretty quickly and we categorized numbers into whether or not they would form a square. We had to make a 3rd category called "Not sure" because students were using very large numbers they couldn't create with the tiles.
Talking About Square Roots

I kids place a few more perfect squares and finally presented them with √7. The student who I gave the card to placed it between 3 and 4 which I couldn't have planned better...it allowed great conversation between students about the differences between square rooting and dividing by 2.
Eventually, I started rolling dice to randomly choose numbers for them to square root and place on their number line. (I used a 10 sided die and a 30 sided die to make 2 and 3 digit numbers.) For those students who caught on quickly, I had them try to approximate the square root to a decimal as accurately as they could.
Overall, I think the lesson went well. The students were engaged and the different tasks allowed me to have conversations with those students who were struggling and let those kids who understood have little competitions among themselves to see who could come up with the most accurate placement on the number line.


 RSS Feed
RSS Feed
